Variational Inference

Motivation

VAE 기반 추천 시스템 (Variational Autoencoder for Collaborative Filtering) 에서

x: 유저의 시청 기록 = [1, 0, 0, 1, 1, 0, …] (영화 클릭 여부 벡터)
z: 유저의 잠재 성향/임베딩 (ex. 로맨스를 좋아함, 액션은 별로 안 좋아함)

유저가 어떤 잠재 변수를 가졌는 지 알면, 비슷한 분포의 유저에게 같은 영화를 추천해 줄 수 있다! 즉, \(p(z \mid x)\)를 구해야 한다. 하지만, \(p(z\mid x)\)를 직접 구하는 것은 매우 어렵다.

\(p(z \mid x) = \frac{p(x, z)}{p(x)}\)인데, \(p(x) = \int p(x, z) dz\) \(p(x)\)는 intractable

MCMC를 사용하면 해결되긴 하지만, 속도가 너무 느림

Idea

posterior 분포 \(p(z \mid x)\) 를 적당히 근사할 수 있는 분포 \(q(z)\)로 대체해서 복잡한 계산을 없애자.

여기서 \(q(z)\)는 우리가 다루기 쉬운 분포를 사용하자. ex. gaussian, GMM, beta 등
분포의 파라미터(ex. \(\mu, \sigma\))를 적당히 바꿔가면서 \(p(z \mid x)\)랑 가장 유사해지는 분포를 찾자.

\(q(z) \approx p(z\mid x)\)가 되게끔 KL divergence를 최소화하는 방법으로 구할 수 있다.

\[q^*(z) = \arg \min_q \, \text{KL}(q(z) \,\|\, p(z\mid x))\]

여기서, ELBO를 최대화 하는 방법으로 KL을 divergence를 최소화 할 수 있다.

KL divergecne의 정의에 의해,

\[\begin{aligned} D_{\text{KL}}(q(z) \parallel p(z \mid x)) &= \mathbb{E}_{q(z)} \left[ \log \frac{q(z)}{p(z \mid x)} \right] \\ &= \mathbb{E}_{q(z)} \left[ \log q(z) - \log p(x, z) + \log p(x) \right] \\ &= \mathbb{E}_{q(z)} \left[ \log q(z) - \log p(x, z) \right] + \log p(x) \\ \end{aligned}\]

따라서,

\[\log p(x) = \mathbb{E}{q(z)} \left[ \log p(x, z) - \log q(z) \right] + D{\text{KL}}(q(z) \parallel p(z|x))\] \[\log p(x) = \mathcal{L}(q) + D_{\text{KL}}(q(z) \parallel p(z|x))\]

ELBO는 다시, 다음과 같이 나타낼 수 있다.

\[\mathcal{L}(q) = \mathbb{E}_{q(z)}\left[ \log \frac{p(x, z)}{q(z)} \right]\] \[\log \frac{p(x, z)}{q(z)} = \log \frac{p(x \mid z)p(z)}{q(z)} = \log p(x \mid z) + \log \frac{p(z)}{q(z)}\] \[\begin{aligned} \mathcal{L}(q) &= \mathbb{E}_{q(z)} \left[ \log p(x \mid z) + \log \frac{p(z)}{q(z)} \right] \\ &= \mathbb{E}{q(z)}[\log p(x \mid z)] + \mathbb{E}{q(z)}\left[\log \frac{p(z)}{q(z)}\right] \end{aligned}\] \[\mathcal{L}(q) = \mathbb{E}{q(z)}[\log p(x \mid z)] - D{\text{KL}}(q(z) \parallel p(z))\]

첫 번째 항은 “잠재 변수 z가 분포 q(z)를 따른다고 가정할 때, z로부터 x를 설명하는 로그확률의 평균”을 의미한다.

두 번째 항은 잠재 변수 \(z\)가 인코더 \(q(z \mid x)\) 에서 너무 “마음대로” 분포를 갖지 않도록 사전 분포 p(z)에 가깝게 유도하는 정규화(regularization) 역할을 한다.

ELBO 최대화
\[argmax_q ELBO = argmax_q E[logp(x \mid z) + logp(z)] - E[logq(z)]\]
여기서 q는 다변량 함수이다. 변수들 간 correlation이 존재하고 서로 다른 분포의 joint를 구하는 것은 매우 어렵다.

MFVI (Mean Field Variational Inference)

분포간의 correlation을 모두 무시하고, 변수들을 독립적으로 근사하자.

\[q(z) = \prod_{j=1}^{J} q_j(z_j)\] \[ELBO = -KL[q_j \mid \exp(\mathbb{E}_{i \ne j}[\log p(x, z)])] + C\]

따라서, KL divergence를 최대화 하기 위해선,

\[q_j(z_j) \propto \exp \left( \mathbb{E}_{i \ne j}[\log p(x, z)] \right)\]

확률 분포로 만들기 위해 아래처럼 정규화(normalizing constant)를 붙여준다.

\[q_j(z_j) = \frac{\exp(\mathbb{E}{i \ne j}[\log p(x, z)])}{\int \exp(\mathbb{E}{i \ne j}[\log p(x, z)]) dz_j}\]

각 \(j\)에 대해:

다른 모든 \(q_i\)를 고정
\(q_j\)만 업데이트
1, 2의 과정을 ELBO가 수렴할 때까지 반복한다.

Monte Calro Approximation

기대값을 계산할 수 없을 때, 샘플링을 통해 근사하는 방법

Motivation

어떤 확률분포 \(p(\theta)\) 아래에서, 어떤 함수 \(f(\theta)\)의 평균을 알고 싶은 상황.

\(\mathbb{E}_{p}[\theta] = \int \theta \cdot p(\theta) \, d\theta\) 이런 형태의 계산은 머신러닝, 베이지안 추론, 강화학습 등에서 자주 등장한다.

Idea

적분 대신 샘플 몇 개 뽑아서 평균을 내자.

\(\mathbb{E}{q(z)}[\log p(x|z)] \approx \frac{1}{L} \sum_{l=1}^{L} \log p(x \mid z^{(l)}), \quad z^{(l)} \sim q(z)\)

\(z\)를 \(q(z \mid x)\)에서 샘플링한다.
디코더 \(p(x \mid z)\)에 넣는다.
log likelihood 계산한다.
- 보통 \(L = 1 \sim 5\) 정도만 해도 잘 작동한다.

Sampling

Inverse CDF

특정 분포를 샘플링 하기 위해서, \(z \sim Uniform(0,1)\) 의 z를 transformation을 통해 우리가 원하는 분포로 옮겨주자. 원하는 분포 T는 어떻게 찾을 수 있을까?

\(T(z) = X\) 가 되도록 하는 \(T\)를 찾아보자.

\[F_X(x) = p(X\geq x) = p(T(z)\geq x) = p(z \geq T^{-1}(x)) = T^{-1}(x)\] \[F_X(x) = T^{-1}(x)\] \[T(x) = F_X^{-1}(x)\]

분포가 복잡할 때, Inverse CDF를 구하기 어렵다는 단점이 있다.

Rejection Sampling

우리가 샘플링하고 싶은 분포:

\[p(z) = \frac{1}{Z_p} \tilde{p}(z)\]

\(\tilde{p}(z)\): unnormalized density (비정규화 상태)
\(Z_p\): 정규화 상수 (보통 모름)
이런 상황에서는 Rejection Sampling을 사용한다.

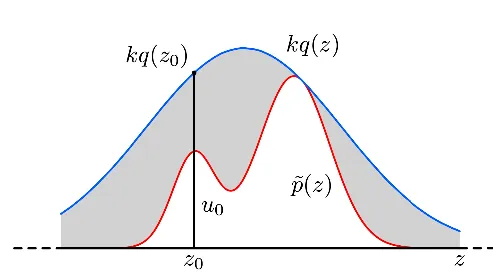
Proposal 분포 \(q(z)\)와 scaling factor \(k\)를 사용해 \(kq(z) \geq \tilde{p}(z)\) 가 되는 범위를 덮도록 한다.

\(z_0 \sim q(z)\) 에서 샘플링
\(u_0 \sim \text{Uniform}(0, kq(z_0))\).
\(u_0 \leq \tilde{p}(z_0)\)이면 accept, 아니면 reject

accept될 확률: \(p(\text{accept}) = \int \frac{\tilde{p}(z)}{kq(z)} q(z) dz = \frac{1}{k} \int \tilde{p}(z) dz\)

수식 유도

\[p(\text{accept} \mid z) = \int_0^{\tilde{p}(z)/kq(z)} \frac{1}{kq(z)} du = \frac{\tilde{p}(z)}{kq(z)}\] \[q(z) p(\text{accept} \mid z) = \frac{\tilde{p}(z)}{k}\] \[kp(\text{accept}) = \int \tilde{p}(z) dz = Z_p\] \[p(z) = \frac{\tilde{p}(z)}{Z_p} = \frac{q(z) \cdot p(\text{accept} \mid z)}{p(\text{accept})}\]

→ rejection sampling을 통해 \(p(z)\)에서 제대로 샘플링한 것과 같아진다!

단점
- 고차원에서는 \(k\)를 매우 크게 잡아야 함
- reject 비율이 커지고, 학습이 느려짐
- → 고차원에선 비효율적이다

Importance Sampling

기대값이 알고싶을 때 사용, 기대값 근사.

\[E[f] = \int f(z)p(z)dz \rightarrow E[f] \approx \sum^L_{l=1}p(z^{(l)})f(z^{(l)})\] \[E(f) = \int f(z)\frac{p(z)}{q(z)}q(z)dz \rightarrow E[f] \approx \frac{1}{L}\sum^{L}_{l=1}\frac{p(z^{(l)})}{q(z^{(l)})}f(z^{(l)})\]

proposal \(q(z)\) 가정. \(q(z)\)에서 sampling

\(\tilde{p}(z)\)와 \(\tilde{q}(z)\)를 통해 구할 수 있다. 상수배 한 비율만 구할 수 있음. \(\tilde{r_l} = \tilde{p}(z^{(l)})/\tilde{q}(z^{(l)})\)

MCMC (Markov Chain Monte Carlo)

Motivation

Variational Inference는 정확한 posterior 샘플링이 불가능함.

rejection sampling, importance sampling은 high-dimensional 문제에서 잘 작동하지 않음.

Idea

proposal distribution \(q(z)\)을 설정한다.
이전 샘플 \(z^{(m)}\)에 기반해 새로운 \(z^{(m+1)}\)를 생성한다.
이 과정을 반복하면, 생성된 샘플 분포가 posterior \(p(z \mid x)\)로 수렴한다.

기존 Monte Carlo는 \(q(z)\)를 고정하고 샘플링하지만,
MCMC는 \(q(z)\)를 매 스텝마다 이동시키며 적응적으로 \(p(z)\)를 근사한다.

Markov Chain

다음 상태 \(z^{(m+1)}\)는 오직 현재 상태 \(z^{(m)}\)에만 의존한다.

\[p(z^{(m+1)} \mid z^{(m)}, z^{(m-1)}, \dots, z^{(0)}) = p(z^{(m+1)} \mid z^{(m)})\]

따라서 초기 확률과, 전이 확률만 있으면 모든 샘플을 만들어 낼 수 있다.

즉, \(p(z)\)를 stationary distribution으로 갖는 마르코프 체인을 만드는 것이 목표이다.

Stationary Distribution

목표: 마르코프 체인의 분포가 수렴하여 posterior 분포 \(p(z \mid x)\)가 되는 것
\[p^*(z) = \sum_{z'} T(z', z) p^*(z')\]
Detailed Balance Equation: \(p^*(z) T(z, z') = p^*(z') T(z', z)\)

이 조건을 만족하면 \(p^*(z)\)는 stationary 함.

수렴 조건 모든 Markov Chain이 수렴하는 것은 아니다.
수렴하려면 다음 두 조건이 필요함:
- Irreducible: 모든 상태 쌍 간 전이 가능
  \(p(z^{(m)} = b \mid z^{(1)} = a) > 0\)
- Aperiodic: 특정 주기 없이 상태를 다시 방문 가능
  \(\gcd(m : p(z^{(m)} = a \mid z^{(1)} = a) > 0) = 1\)

Metropolis-Hastings Algorithm

기본 Metropolis Proposal: 대칭 분포 \(q(z^*|z) = q(z|z^*)\)
\[A(z^*, z^{(\tau)}) = \min\left(1, \frac{\tilde{p}(z^*)}{\tilde{p}(z^{(\tau)})}\right)\]
Metropolis-Hastings (일반화된 MH)
\[A_k(z^*, z^{(\tau)}) = \min\left(1, \frac{\tilde{p}(z^*) q_k(z^{(\tau)} \mid z^*)}{\tilde{p}(z^{(\tau)}) q_k(z^* \mid z^{(\tau)})}\right)\]
- \(q_k(z^* \mid z^{(\tau)})\): asymmetric proposal 분포
- MH는 detailed balance를 만족하므로 \(p(z)\)로 수렴함
- 단점
  - proposal 분포의 variance가 너무 크면 → 거의 다 reject됨
  - variance가 작으면 → 샘플 이동이 느림 (convergence 느림)
  - 고차원에서는 변수마다 적절한 variance 조절이 어려움

Gibbs Sampling

각 변수에 대해 조건부 분포를 순차적으로 샘플링
특히 high-dimensional 문제에서 효과적
기본 아이디어
\[p(x, y) \Rightarrow \text{직접 샘플링 어려움} \Rightarrow p(x \mid y),\; p(y \mid x) \text{ 로 분할 샘플링}\]
- 항상 accept됨 (reject 없음)
- Markov blanket 기반으로 조건부 독립 구조를 활용
Markov blanket:
해당 변수의 부모 + 자식 + 자식의 부모로 구성됨

HMC (Hamiltonian Monte Carlo)

단순한 랜덤 걷기 대신, 물리 기반 운동량 정보를 이용해서 더 효율적으로 샘플링

구성 요소
- \(x\): 위치(position), \(w\): 운동량(momentum)
- 총 에너지 함수 (Hamiltonian):
\[H(x, w) = U(x) + K(w)\]
Hamiltonian Dynamics:

\[\frac{dx}{dt} = \frac{\partial H}{\partial p}, \quad \frac{dp}{dt} = -\frac{\partial H}{\partial x}\]

작동 방식
1. 무작위 운동량 \(w_0\) 샘플링
  \(p(w) \propto \exp(-V(w))\)
2. Leapfrog 통합법으로 \(x, w\)를 시간 단위 \(\epsilon\)만큼 업데이트
3. MH-style accept/reject
\[a(x_0, w_0, x_T, w_T) = \min\left(1, \frac{\exp(-H(x_T, w_T))}{\exp(-H(x_0, w_0))} \right)\]
- 에너지가 보존되므로 accept 비율이 높음
- detailed balance 만족 → posterior 수렴 보장